|
|
| |
|
|
Summarized the route techniques we use at scouting are nothing more than a form of cryptography. They are written with the goal to guide
people form A to B.
The originator of the route has an endpoint in mind, and participants must interpret and get to the endpoint.
It is an exercise for writer and participant in the communication between both parties.
By making the participants walk in groups, they not only train interpreting skills, they allso train cooperation and togetherness.
Disagreements on interpretation or worse, walking th wrong way, creates friction in these groups.
Staff should therefore find a challenge, to make the perfect route.
The techniques, derived from the army, are a part of the standard knowledge, with minimum effort it is possible to convert them into something new,
and give it a different look. For the following it is important that you are familiar with the basics of navigating (compass, degrees rose,
wind direction and protractor card)
Situation
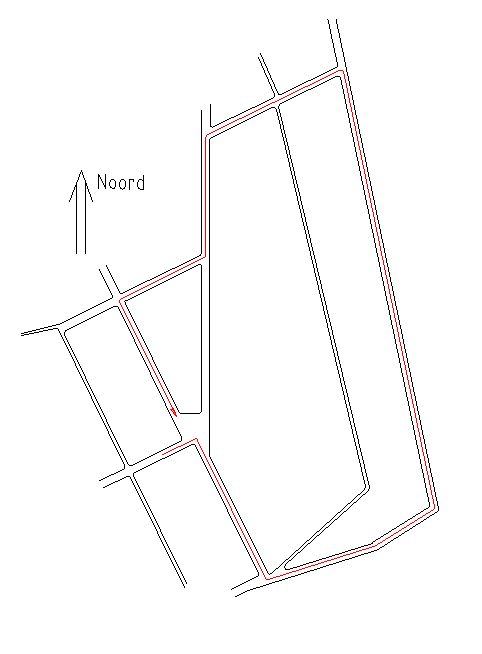
At the right, a situation as you may encounter on a map. In red a possible route wich is translated into techniques as you go down. |
| |
|
Description
|
| Summarized the route techniques we use at scouting are nothing more than a form of cryptography. They are written with the goal to guide
people form A to B.
The originator of the route has an endpoint in mind, and participants must interpret and get to the endpoint.
It is an exercise for writer and participant in the communication between both parties.
By making the participants walk in groups, they not only train interpreting skills, they allso train cooperation and togetherness.
Disagreements on interpretation or worse, walking th wrong way, creates friction in these groups.
Staff should therefore find a challenge, to make the perfect route.
The techniques, derived from the army, are a part of the standard knowledge, with minimum effort it is possible to convert them into something new,
and give it a different look. For the following it is important that you are familiar with the basics of navigating (compass, degrees rose,
wind direction and protractor card)
Situation
At the right, a situation as you may encounter on a map. In red a possible route wich is translated into techniques as you go down. |
| |
|
Intersection Route
|
In routebooks, the route descriptions are often clarified with a sketch of each intersection.
These can individually sketch the route the form is then called a crossing route.
Additional difficulty can be obtained by placing every intersection North.
 |
| |
|
Helicopter Route
|
When you remove the crossroad situations and combine all arrows you get something called the helicopter route.
If all arrows are of equal length, it is a route from traffic crossing to trafic crossing.
When the arrows vary in length, the arrows are drawn to scale. Traditional 1:25 000
The figures show the individual junctions, on the right, the entire route in one sketch.
 |
| |
|
Clock_Route
|
A variant of the helicopter route is easily made by processing the individual crossings into a watch.
The hour hand displays the North, while the minutes indicate the direction you need to follow.
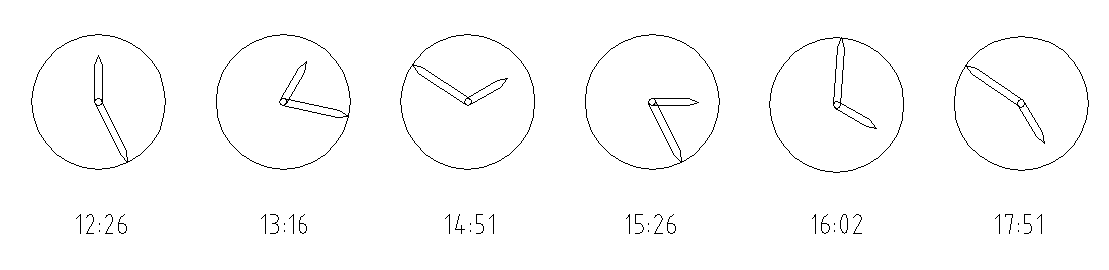The difficulty is increased when we make it digital:
12:26uur, 13:16uur, 14:51uur, 15:26uur, 16:02uur; 17:51uur. |
| |
|
Ball-Arrow
|
This is again an arrow-marked route, where you come from (the ball) and where you need to go back (arrow).
Since you have the situation clear, it is difficult to estimate whether you are going in the right direction.
The difficulty can again be increased by working with straight arrows. From Bottom to the top of the assignment-sheet
the direction is displayed. The arrow indicates the direction that you need to go. |
| |
|
Balls Route
|
With a balls route you get the direction you need for every situation.
The notation is that clumps with a hyphen is attached. The dash gives a ball a wind direction.
A circle with a line upwards displays North, and so on. Through a combination of three balls, reading from bottom to top, you can refine it.
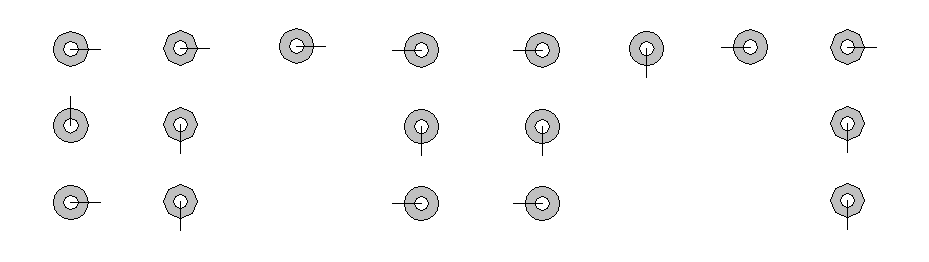to read as:
E.N.E S.S.O East W.S.W W.S.W South West S.S.O |
| |
|
Striping
|
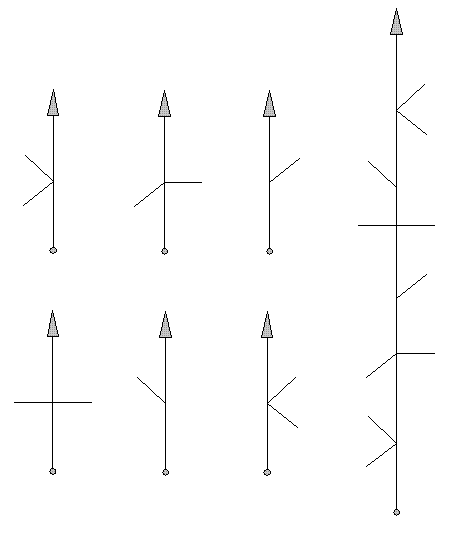The stripingroute is also read from bottom to top. The route dous not display the path to follow, but the paths you should leave.
From left to right individual intersections.
Leave two paths on your left, Leave a path on your left and simultaniously one on the right,
Leave a path on your right, Leave a path on your left and simultaniously one on the right, Leave a path on your left, Leave two paths on your right.
Far right the entire route. |
| |
|
Oleate
|
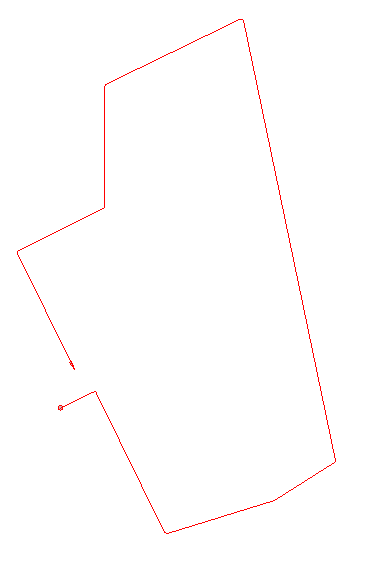By transferring a route from a map to a clear plastic, you get an oleate.
This indicates the start and end point on the map. If no card is present it is called a blind oleate.
Anyone who follows this route technique will therefore have to relate on angles and distances.
An additional challenge is when the competitor has to determin his own starting direction. (Blind Oleate) |
| |
|
Binairy
|
A computer calculates binary. It transforms a number to a combination of 0's and 1's. To understand the transformation proces: A 0 stands for
switch off and a 1 stands for switch on. The values wich to be used are displayed in the table.
|
| Binairy code |
| 27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| 128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
| Example |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
The combination (01100010) stands for 64+32+2 = 98. The biggest number available in this way is 255 (one byte in this 8 bit code).
To be able to use larger numbers we will have to calculate, or switch to a 16 bit code. The last one will increase the table.
With the math you will have to know 1+0=0 1+1=10 1+1+1=11
|
| Binairy code |
| 27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
|
| 128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
| Example 98+98=196 |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
+ |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
+ |
|
|
With this knowledge you can now transform coördinates or numbers in a route-technique.
No example made. |
| |
|
Fibonacci
|
The row of Fibonacci is named after, Leonardo da Pisa (born in 1170 at Pisa, Italy). The family of Leonardo were called Bonacci, seen it was
usual to call themselves Son of Bonacci (Filius Bonacci, in short Fibonacci)., Leonardo got known as Fibonacci.
Fibonacci's influence was underastimated in Mathemathics, as in 1170 not many had an interest in science.
Global interest in his work now contributes to his fame as his work is known in modern mathemathical science. Search for more about his
spiral code to understand the image.
The row of Fibonacci can be best used to code numbers. For this reason I made it a route-technique and not as a Cryptography.
The row is a infinate row of numbers , wich follows in a recursive formula; a formula wich can be repeated without an ending, a formula wich
effectively adds natural numbers to natural numbers.
This means: a statement gets calculated based on previous statements.
Mathematically:a(n) gets calculated by a(n-1) and a(n-2) as: a(n) = a(n-1) + a(n-2).
Or in normal language: A row of numbers started with 0 and 1 in wich the next statement is made out of the sum of the two prious numbers.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, (Fibonacci-row)
The Fibonacci-nummer is the position in the fibonacci-sequence noted as F("number"), in this way F(8) equals the value 21.
|
| Fibonacci-table |
| Number |
Fibonacci |
|
Number |
Fibonacci |
| 0 |
F(0) |
|
55 |
F(10) |
| 1 |
F(1) |
|
89 |
F(11) |
| 1 |
F(2) |
|
144 |
F(12) |
| 2 |
F(3) |
|
233 |
F(13) |
| 3 |
F(4) |
|
377 |
F(14) |
| 5 |
F(5) |
|
610 |
F(15) |
| 8 |
F(6) |
|
987 |
F(16) |
| 13 |
F(7) |
|
1597 |
F(17) |
| 21 |
F(8) |
|
2584 |
F(18) |
| 34 |
F(9) |
|
4181 |
F(19) |
|
| Route example, Dutch RD coördinate |
| You are at RD F(12)+8,F(6) - F(4)71,F(0) |
| Start by going E.N.E. |
| Go F(12)+6º East, over adistance of F(12)+36 mtr |
| Take the F(3) way left on the intersection |
| Go F(10)*2º West, over adistance of F(12)+36 mtr |
| Go 182º East, over adistance of F(12)-4 mtr |
| Stay on the heading S.S.E |
|
|
|
|
|
|
| |
