|
|
|
|
De routetechnieken die we bij scouting toepassen zijn kort samengevat niets meer dan een vorm van geheimschrift. Het zijn echter geschriften met een specifiek doel.
De opsteller van de route heeft een eindpunt voor ogen en de deelnemers dienen zijn schrift te interpreteren en zo op het eindpunt te geraken. Het is dus een oefening voor schrijver en deelnemer in communicatie tussen beide partijen.
Door de deelnemers in groepen te laten lopen, wordt naast de traing in interpretatie van dit geschift, ook samenwerking en samenhorigheid gestimuleerd.
Bij onenigheid over interpretatie of erger nog, verkeerd lopen, ontstaat wrijving in deze groepen.
Voor stafleden zou het daarom een uitdaging moeten zijn om een route, goed, uit te zetten. De gebruikte technieken, afgeleid van die uit het leger, horen bij de standaard kennis maar zijn met minimale
moeite vaak om te zetten naar iets wat nieuw en anders oogt. Voor onderstaande is van belang dat je bekend bent met de basis van Navigeren (windroos,
gradenroos, kompas en kaarthoekmeter).
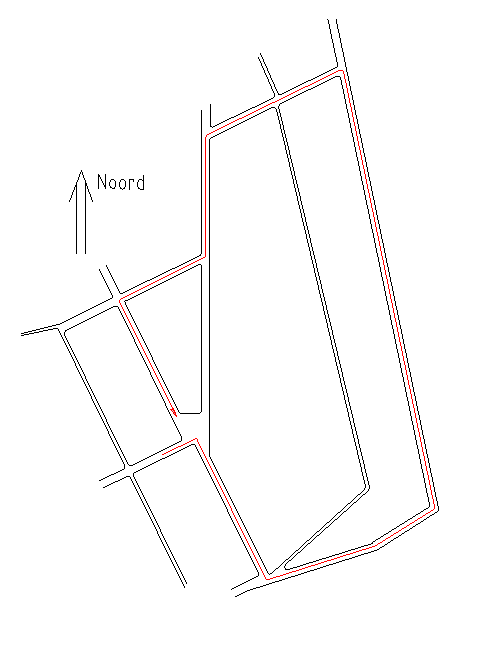
Situatie
Rechts is een mogelijke situatie getekend zoals je deze op een landkaart aan kunt treffen. Hier is (in rood) een mogelijke route aangegeven. Deze route is hieronder vertaald naar routetechnieken en hun uitleg. |
| |
|
Routeomschrijving
|
| In een routeomschrijving wordt je exact verteld, wat je dient te ondernemen om op de plaats van bestemming te geraken.
Het uitgangspunt voor de opdracht is altijd de aanlooprichting. Zorg dat je dus altijd onthoud waar je vandaan komt. Begrippen als rechtdoor,
links of rechts worden anders wel heel moeilijk. Lijkt makkelijk genoeg, maar wat nu als je een variant krijgt? |
| Omschrijving |
windrichting |
In graden (Oost om) |
In graden (West om) |
| Laat je in een richting wijzen |
Vertrek in O.N.O. richting |
Ga 70º Oost om, 50 mtr |
Ga 290º West om, 50 mtr |
| Neem de eerste afslag rechts |
Ga Z.Z.O |
Ga 150º Oost om, 180 mtr |
Ga 210º West om, 180 mtr |
| Op viersprong tweede weg links |
Ga Oost |
Ga 70º Oost om, 720 mtr |
Ga 290º West om, 720 mtr |
| Neem de eerste afslag naar links |
Ga W.Z.W |
Ga 250º Oost om, 80 mtr |
Ga 110º West om, 180 mtr |
| Neem de tweede afslag naar links |
Ga W.Z.W en ga Zuid |
Ga 250º Oost om, 100 mtr |
niet, zit reeds in vorige |
| Neem de eerste afslag naar rechts |
Ga West |
Ga 182º Oost om, 140 mtr |
Ga 178º West om, 140 mtr |
| Neem de eerste afslag naar links |
Ga Z.Z.O |
Ga 246º Oost om, 110 mtr |
Ga 114º West om, 110 mtr |
| |
|
Ga 158º Oost om, 150 mtr |
Ga 202º West om, 150 mtr |
|
| |
|
Kruispuntenroute
|
In routeboeken zal de routeomschrijving vaak verduidelijkt zijn met een schets van ieder kruispunt.
Deze afzonderlijke schets kan ook alleen de route vormen en heet dan een kruispuntenroute.
Extra moeilijkheidsgraad kan worden verkregen, door ieder kruispunt op noord te richten.
 |
| |
|
Helicopterroute
|
Wanneer je van de kruispuntenroute de situaties af haalt en alle richtingpijlen combineert noemen we het een helicopterroute. Als alle
richtingspijlen even lang zijn, geldt dat er van kruising naar kruising gelopen wordt. Wanneer de pijlen varieeren in lengte dienen de
pijlen op schaal getekend te zijn. traditioneel 1:25 000. De figuren laten de afzonderlijke kruisingen zien, geheel rechts de complete
route in een tekeningetje.
 |
| |
|
Klokkenroute
|
Een variant op de Helicopterroute is eenvoudig gemaakt door de afzonderlijke kruisingen te verwerken in een uurwerk.
De uurwijzer geeft het Noorden aan, terwijl de minutenaanduiding de richting is die je moet volgen.
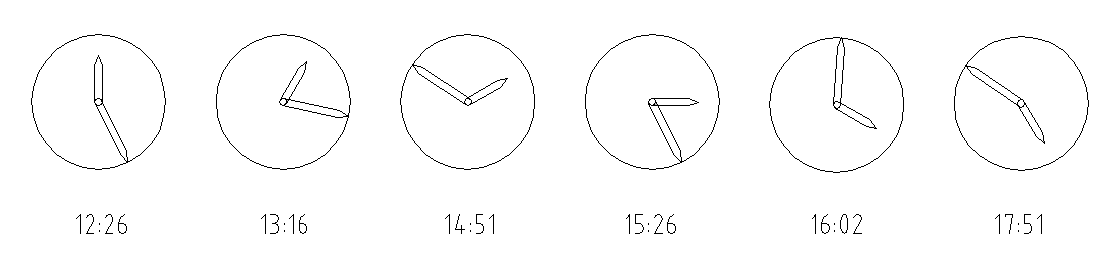De moeilijkheidsgraad wordt aanzienlijk verhoogd wanneer dit digitaal gemaakt wordt:
12:26uur, 13:16uur, 14:51uur, 15:26uur, 16:02uur; 17:51uur. |
| |
|
Bolletje-Pijltje route
|
Bij een Bolletje-pijltje route wordt aangegeven waar je vandaan komt (het bolletje) en waar je weer heen moet (de pijl).
Aangezien je de situatie niet inzichtelijk hebt is het moeilijk inschatten of je wel de goede kant in gaat.
De moeilijkheidsgraad kan weer worden verhoogd door met rechte pijlen te werken. Van onder naar de bovenzijde van het
opdrachtenblad is dan de huidige looprichting. De pijl geeft de richting aan die je in moet. |
| |
|
Bolletjesroute
|
Bij een bolletjes route krijg je voor iedere situatie de windrichting die je in moet.
De notatie gebeurt met polletjes waaraan een streepje verbonden zit. Het streepje geeft per bolletje een windrichting aan.
Een cirkel met een streepje naar boven geeft dus Noord aan. Door een combinatie van drie bolletjes, van onder naar boven te lezen,
kun je verfijnen.
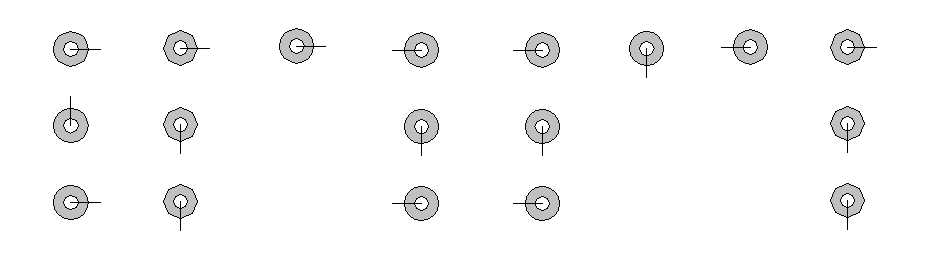te lezen als:
O.N.O Z.Z.O Oost W.Z.W W.Z.W Zuid West Z.Z.O |
| |
|
Strippenroute
|
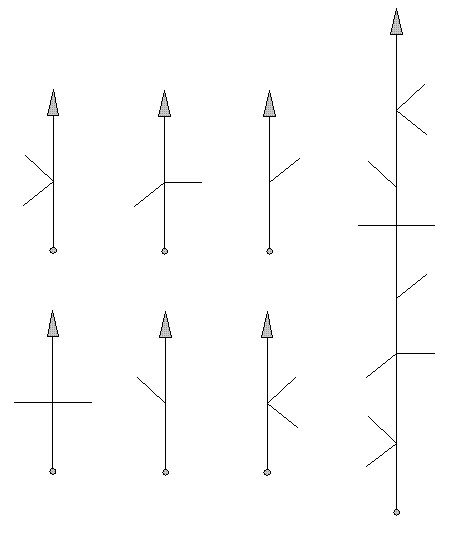De strippenroute wordt eveneens van onder naar boven gelezen. Bij een Strippenroute worden echter niet de te volgen wegen weergegeven, maar de wegen die je dient te laten liggen.
Van links naar rechts de afzonderlijke kruispunten. Laat twee wegen links liggen, Laat een weg links en een weg rechts liggen, laat een weg rechts liggen, Laat een weg links en een weg rechts liggen, Laat een weg links liggen, Laat twee wegen rechts liggen.
Geheel rechts de complete route. |
| |
|
Oleaat
|
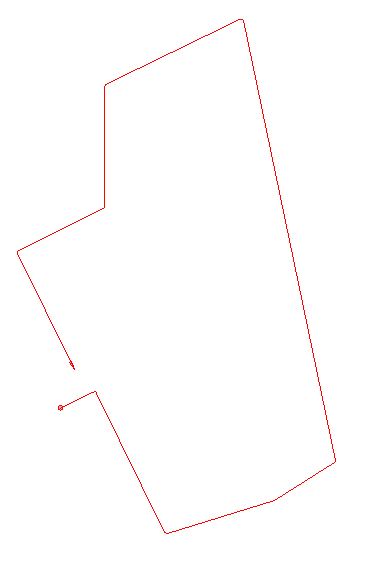Door je route op een doorzichtig plastic over te trekken, van een landkaart, verkrijg je een oleaat. Deze geeft het begin en eindpunt aan
op kaart. Wanneer er géén kaart aanwezig is noemen we het een blind oleaat. Degene die deze routetechniek volgt zal dus af moeten gaan op
onderlinge hoeken en afstanden. Een extra uitdaging is het wanneer de deelnemer zijn eigen startrichting moet gaan bepalen. |
| |
|
Binaire-route
|
Het binaire-stelsel is dat wat een computer gebruikt om te kunnen rekenen. Het zet een getal om naar combinaties van 0-en en 1-en. Om te weten hoe
je deze combinaties om telt zul je moeten weten hoe dit werkt. Een 0 staat voor de schakelaar uit en de 1 staat voor een schakelaar aan. De waarden
die je zo kunt verkrijgen staan in onderstaande tabel. Het voorbeeld wordt onder de tabel uitgelegd
|
| Binaire code |
| 27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
| 128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
| Voorbeeld |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
De verkregen combinatie (01100010) staat voor 64+32+2 = 98. Het grootste getal is echter 255 (een byte in deze 8 bits code).
Om groter getallen weer te geven zullen we moeten rekenen. Of overschakelen naar een 16-bits code. Hiervoor zul je de tabel moeten vergroten.
Bij het tellen dien je er rekening mee te houden dat 1+0=0 1+1=10 1+1+1=11
|
| Binaire code |
| 27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
|
| 128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
| Voorbeeld 98+98=196 |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
+ |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
+ |
|
|
Met deze wetenschap kun je nu getallen in een coördinaat of getallen in een routetechniek
anders weergeven.
Géén voorbeeld uitgewerkt. |
| |
|
Fibonacci
|
De rij van Fibonacci is genoemd naar, Leonardo da Pisa (geboren in 1170 te Pisa, Italië), De familie van Leonardo heette Bonacci, en daar het in die
tijd gebruikelijk was zichzelf Filius Bonacci (zoon van de Bonacci’s) te noemen, werd Leonardo da Pisa bekend onder de naam Fibonacci.
Fibonacci's invloed op de geschiedenis van de wiskunde wordt veelal onderschat, aangezien men in zijn tijd weinig interesse toonde in de wetenschap.
Een ondertussen wijdverspreide interesse in zijn werk heeft veel bijgedragen aan zijn grote bekendheid. Nog steeds is zijn gedachtegoed
bekend in de moderne wiskunde en niet verloren gegaan na zijn dood omstreeks 1250 in Pisa. Plaatje is aan de lezer uit te zoeken wat het betekend. (Wiskunde kan
ook leuk zijn.)
De Fibonacci-rij kan het beste worden gebruikt voor het versleutelen van getallen. Om deze reden heb ik hem niet opgenomen als geheimschrift maar als
routetechniek. De rij van Fibonacci is een oneindig lange reeks van getallen, die volgt uit een zogenaamde recursieve formule; een formule die onbeperkt herhalend
toepasbaar is, een formule die op een effectieve wijze aan natuurlijke getallen weer natuurlijke getallen toevoegt. Dit wil dus zeggen; een formule
waarmee een term wordt berekend aan de hand van de vórige termen. Bij de rij van Fibonacci telt men voor iedere nieuwe term de vorige twee termen op.
In de wiskunde zegt men: men berekent a(n) door middel van a(n-1) en a(n-2), namelijk: a(n) = a(n-1) + a(n-2).
Of in normale mensen taal: Een rij getallen begonnen met 0 en 1 waarbij het opvolgende element bestaat uit de som van de twee voorgaande.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, (Fibonacci-reeks)
Het Fibonacci-nummer is het positienummer in de fibonacci-reeks genoteerd als F("het nummer"), zo is F(8) gelijk aan de numerieke waarde 21.
|
| Fibonacci-tabel |
| Numeriek |
Fibonacci |
|
Numeriek |
Fibonacci |
| 0 |
F(0) |
|
55 |
F(10) |
| 1 |
F(1) |
|
89 |
F(11) |
| 1 |
F(2) |
|
144 |
F(12) |
| 2 |
F(3) |
|
233 |
F(13) |
| 3 |
F(4) |
|
377 |
F(14) |
| 5 |
F(5) |
|
610 |
F(15) |
| 8 |
F(6) |
|
987 |
F(16) |
| 13 |
F(7) |
|
1597 |
F(17) |
| 21 |
F(8) |
|
2584 |
F(18) |
| 34 |
F(9) |
|
4181 |
F(19) |
|
| Route voorbeeld |
| Je bevind jezelf op RD F(12)+8,F(6) - F(4)71,F(0) |
| Vertrek in O.N.O. richting |
| Ga F(12)+6º Oost om, over een afstand van F(12)+36 mtr |
| Neem op de viersprong de F(3)de weg links |
| Ga F(10)*2º West om, over een afstand van F(12)+36 mtr |
| Ga 182º Oost om, over een afstand van F(12)-4 mtr |
| Vervolg je weg in Z.Z.O richting |
|
|
|
|
|
|
| |
